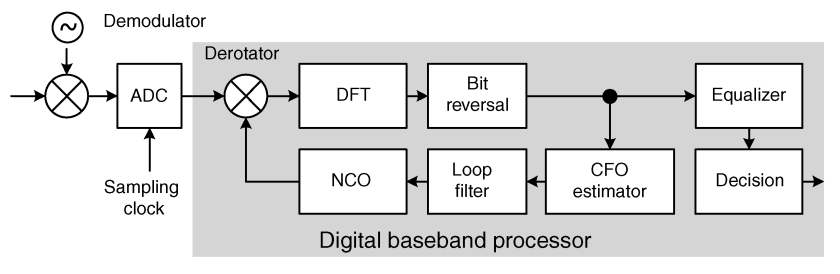
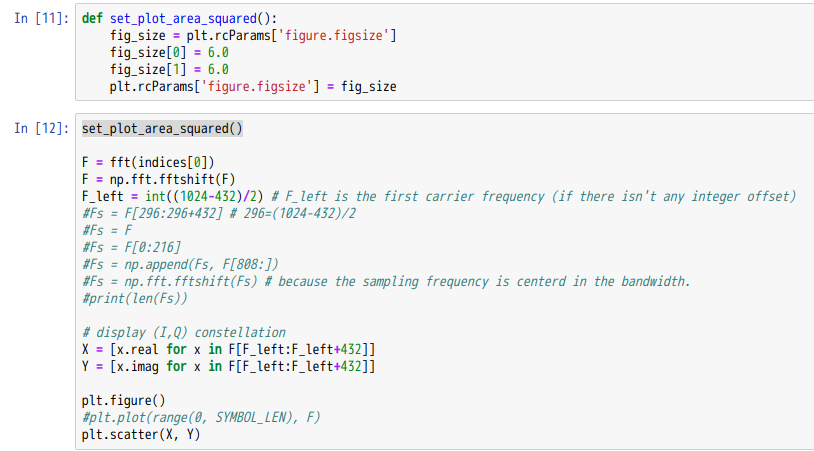
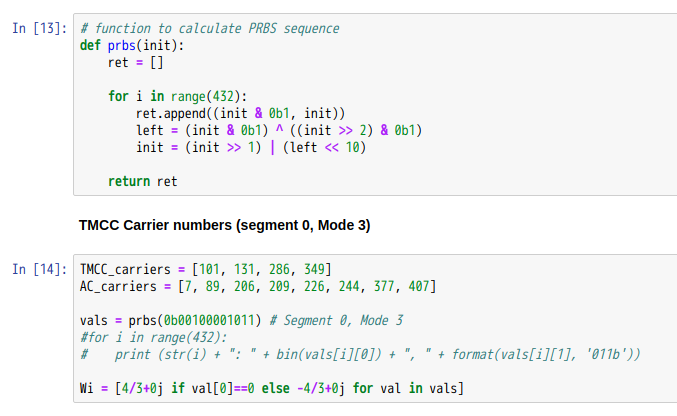
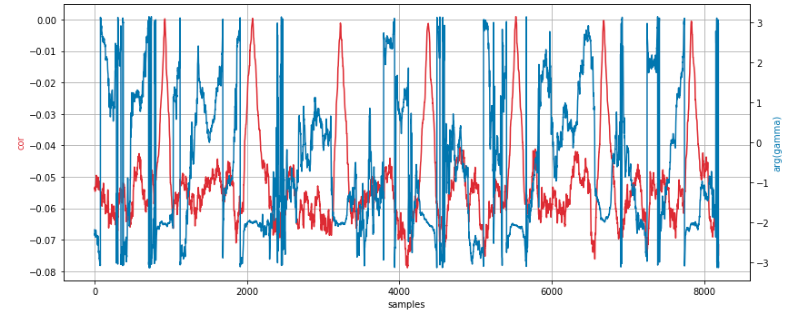
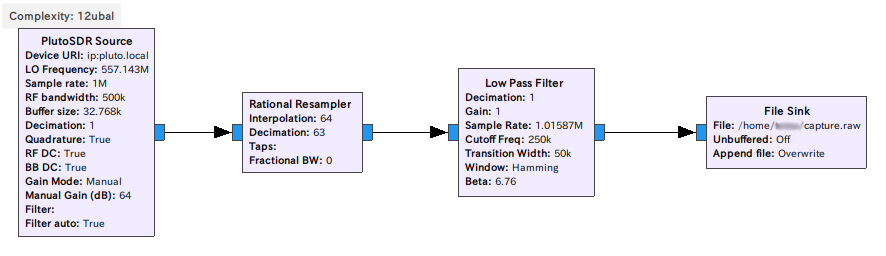
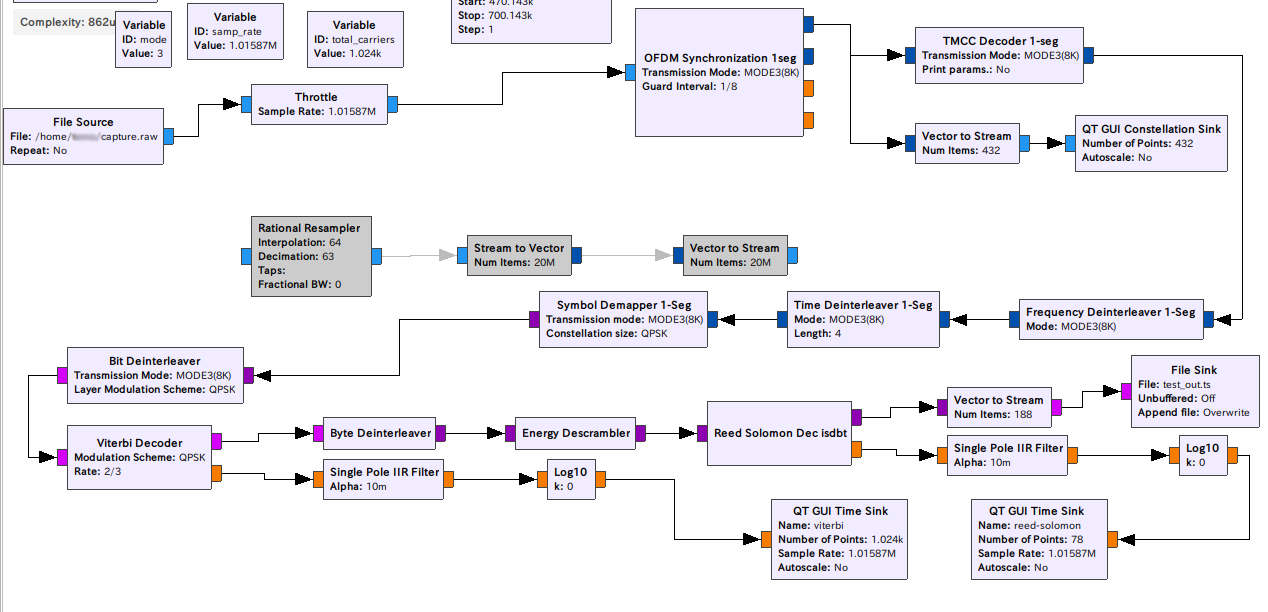
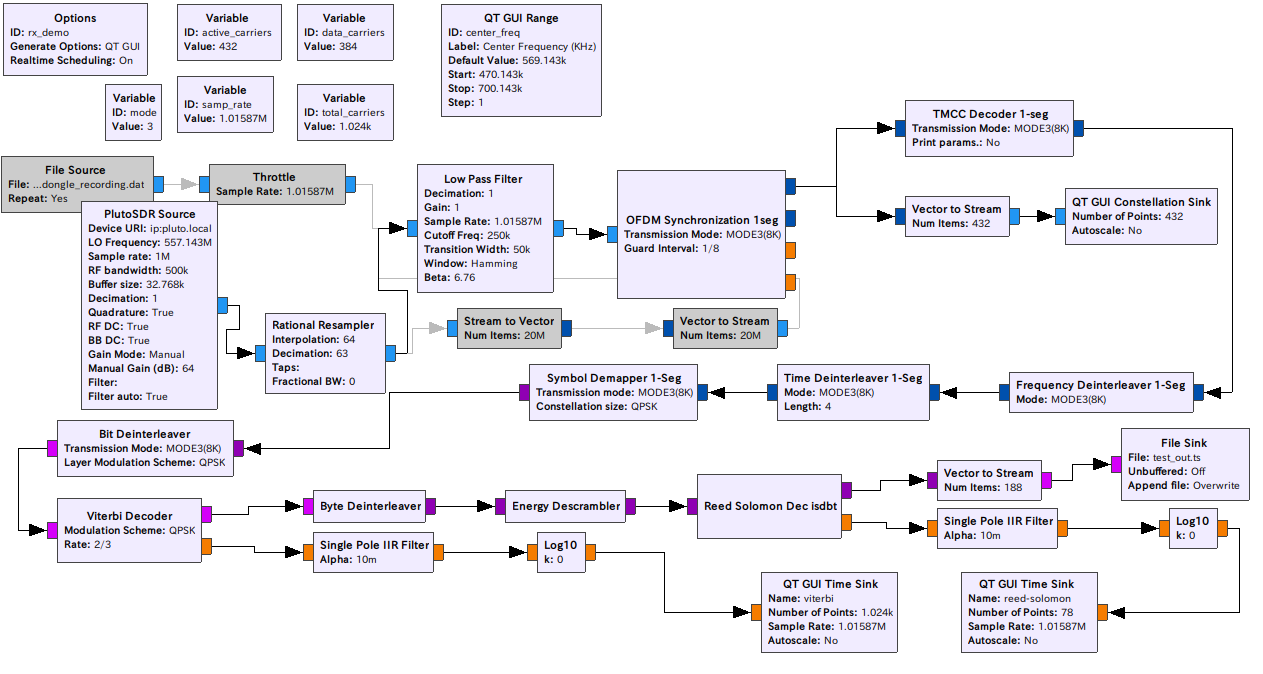
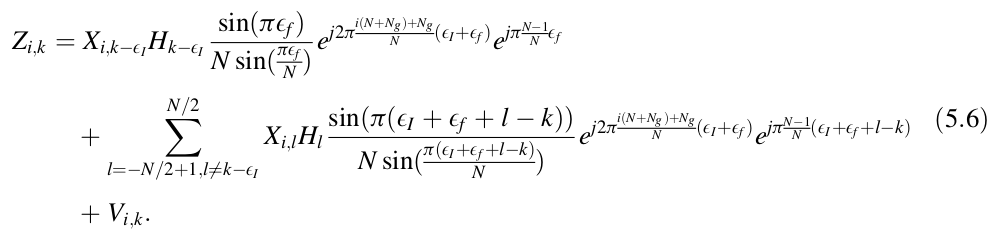Analog DevicesのADALM PLUTOをMouserから購入しました。まだ99USDで買えたようです。
ここはちょっと余談
これに入っているAD9363というデバイスは、
LNA, 直交ミキサ, PLL, フィルタ, ADC, DAC, FIRフィルタなど、RFフロントエンドにおおよそ必要な機能が、
たった一つのICに入っています。本来なら、これらのコンポーネントをそれぞれ基板に配置して設計したほうが楽しそうですが、
かなり骨の折れる作業です。このデバイスなら、たった1つ置くだけで良いわけです。
ただし、高機能な分、お値段も素晴らしいです。Digikeyでは1個14,640円でした(11/5調べ)。
これだけの機能があれば、それほど高くは無いとも言えるのかも知れませんが。
もっとも、実際自分でレジスタを適切に設定するのは結構大変だと予想されます。
それで、メーカはデバイスドライバで簡単に使えるようにしてくれているようです。
ちなみに、これにはXilinxのZynqも入っています。これで私物で買ったZynqは3つ目です…
個々の部品代を考えると、これがたった1万円ちょっとで購入できるわけですので、
遊びで使う分にはかなりお買い得かと思います。
余談終わり

本体に加えて、アンテナ2本とSMAケーブル、USBケーブル(Type-A <-> Micro-Bタイプ)が付属しています。USBケーブルでPCに接続すると、LED1とReadyが光ります。
WikiにあるLinux Driversの内容に従って、libiio-utilsをインストールして
$ iio_info -n 192.168.2.1
すると、次のようなメッセージが表示されました。
Library version: 0.10 (git tag: v0.10)
Compiled with backends: local xml ip usb serial
IIO context created with network backend.
Backend version: 0.14 (git tag: v0.14 )
Backend description string: 192.168.2.1 Linux (none) 4.9.0-10315-gb07f3c6 #234 SMP PREEMPT Tue Apr 24 13:47:24 CEST 20
18 armv7l
IIO context has 8 attributes:
hw_model: Analog Devices PlutoSDR Rev.B (Z7010-AD9363)
hw_model_variant: 0
hw_serial: 104473ce69910015ecff2b0017e78933a0
fw_version: v0.28
ad9361-phy,xo_correction: 40000140
ad9361-phy,model: ad9363a
local,kernel: 4.9.0-10315-gb07f3c6
ip,ip-addr: 192.168.2.1
IIO context has 5 devices:
iio:device3: cf-ad9361-dds-core-lpc (buffer capable)
6 channels found:
voltage0: (output, index: 0, format: le:S16/16>>0)
4 channel-specific attributes found:
attr 0: calibscale value: 1.000000
attr 1: calibphase value: 0.000000
attr 2: sampling_frequency_available value: 30719999 3839999
attr 3: sampling_frequency value: 30719999
voltage1: (output, index: 1, format: le:S16/16>>0)
4 channel-specific attributes found:
attr 0: calibphase value: 0.000000
attr 1: calibscale value: 1.000000
attr 2: sampling_frequency_available value: 30719999 3839999
attr 3: sampling_frequency value: 30719999
altvoltage3: TX1_Q_F2 (output)
5 channel-specific attributes found:
attr 0: raw value: 1
attr 1: phase value: 0
attr 2: frequency value: 9279985
attr 3: scale value: 0.000000
attr 4: sampling_frequency value: 30719999
altvoltage1: TX1_I_F2 (output)
5 channel-specific attributes found:
attr 0: phase value: 90000
attr 1: scale value: 0.000000
attr 2: raw value: 1
attr 3: frequency value: 9279985
attr 4: sampling_frequency value: 30719999
altvoltage0: TX1_I_F1 (output)
5 channel-specific attributes found:
attr 0: phase value: 90000
attr 1: scale value: 0.000000
attr 2: frequency value: 9279985
attr 3: raw value: 1
attr 4: sampling_frequency value: 30719999
altvoltage2: TX1_Q_F1 (output)
5 channel-specific attributes found:
attr 0: raw value: 1
attr 1: phase value: 0
attr 2: frequency value: 9279985
attr 3: scale value: 0.000000
attr 4: sampling_frequency value: 30719999
1 debug attributes found:
debug attr 0: direct_reg_access value: 0x90062
iio:device1: ad9361-phy
9 channels found:
altvoltage1: TX_LO (output)
8 channel-specific attributes found:
attr 0: external value: 0
attr 1: frequency value: 2450000000
attr 2: fastlock_store value: 0
attr 3: fastlock_recall ERROR: Invalid argument (-22)
attr 4: powerdown value: 0
attr 5: fastlock_save value: 0 238,206,235,207,206,253,207,233,206,206,123,253,206,206,206,206
attr 6: frequency_available value: [325000000 1 3800000000]
attr 7: fastlock_load value: 0
voltage0: (input)
15 channel-specific attributes found:
attr 0: hardwaregain_available value: [-3 1 71]
attr 1: hardwaregain value: 71.000000 dB
attr 2: rssi value: 115.75 dB
attr 3: rf_port_select value: A_BALANCED
attr 4: gain_control_mode value: slow_attack
attr 5: rf_port_select_available value: A_BALANCED B_BALANCED C_BALANCED A_N A_P B_N B_P C_N C_P TX_MONITOR1 TX_MONITOR2 TX_MONITOR1_2
attr 6: rf_bandwidth value: 18000000
attr 7: rf_dc_offset_tracking_en value: 1
attr 8: sampling_frequency_available value: [2083333 1 61440000]
attr 9: quadrature_tracking_en value: 1
attr 10: sampling_frequency value: 30719999
attr 11: gain_control_mode_available value: manual fast_attack slow_attack hybrid
attr 12: filter_fir_en value: 0
attr 13: rf_bandwidth_available value: [200000 1 56000000]
attr 14: bb_dc_offset_tracking_en value: 1
voltage3: (output)
8 channel-specific attributes found:
attr 0: scale value: 1.000000
attr 1: raw value: 306
attr 2: sampling_frequency_available value: [2083333 1 61440000]
attr 3: rf_port_select_available value: A B
attr 4: filter_fir_en value: 0
attr 5: sampling_frequency value: 30719999
attr 6: rf_bandwidth_available value: [200000 1 40000000]
attr 7: rf_bandwidth value: 18000000
altvoltage0: RX_LO (output)
8 channel-specific attributes found:
attr 0: frequency_available value: [325000000 1 3800000000]
attr 1: fastlock_save value: 0 244,244,244,244,244,244,244,228,244,244,244,244,244,244,244,252
attr 2: powerdown value: 0
attr 3: fastlock_load value: 0
attr 4: fastlock_store value: 0
attr 5: frequency value: 2400000000
attr 6: external value: 0
attr 7: fastlock_recall ERROR: Invalid argument (-22)
voltage2: (output)
8 channel-specific attributes found:
attr 0: raw value: 306
attr 1: scale value: 1.000000
attr 2: sampling_frequency_available value: [2083333 1 61440000]
attr 3: rf_port_select_available value: A B
attr 4: filter_fir_en value: 0
attr 5: sampling_frequency value: 30719999
attr 6: rf_bandwidth_available value: [200000 1 40000000]
attr 7: rf_bandwidth value: 18000000
temp0: (input)
1 channel-specific attributes found:
attr 0: input value: 36842
voltage0: (output)
10 channel-specific attributes found:
attr 0: rf_port_select value: A
attr 1: hardwaregain value: -10.000000 dB
attr 2: rssi value: 0.00 dB
attr 3: hardwaregain_available value: [0 250 89750]
attr 4: sampling_frequency_available value: [2083333 1 61440000]
attr 5: rf_port_select_available value: A B
attr 6: filter_fir_en value: 0
attr 7: sampling_frequency value: 30719999
attr 8: rf_bandwidth_available value: [200000 1 40000000]
attr 9: rf_bandwidth value: 18000000
voltage2: (input)
13 channel-specific attributes found:
attr 0: offset value: 57
attr 1: scale value: 0.305250
attr 2: raw value: 892
attr 3: rf_port_select_available value: A_BALANCED B_BALANCED C_BALANCED A_N A_P B_N B_P C_N C_P TX_MONITOR1 TX_MONITOR2 TX_MONITOR1_2
attr 4: rf_bandwidth value: 18000000
attr 5: rf_dc_offset_tracking_en value: 1
attr 6: sampling_frequency_available value: [2083333 1 61440000]
attr 7: quadrature_tracking_en value: 1
attr 8: sampling_frequency value: 30719999
attr 9: gain_control_mode_available value: manual fast_attack slow_attack hybrid
attr 10: filter_fir_en value: 0
attr 11: rf_bandwidth_available value: [200000 1 56000000]
attr 12: bb_dc_offset_tracking_en value: 1
out: (input)
1 channel-specific attributes found:
attr 0: voltage_filter_fir_en value: 0
18 device-specific attributes found:
attr 0: dcxo_tune_coarse ERROR: No such device (-19)
attr 1: rx_path_rates value: BBPLL:983039994 ADC:245759998 R2:122879999 R1:61439999 RF:30719999 RXSAMP:30719999
attr 2: trx_rate_governor value: nominal
attr 3: calib_mode_available value: auto manual manual_tx_quad tx_quad rf_dc_offs rssi_gain_step
attr 4: xo_correction_available value: [39992140 1 40008140]
attr 5: gain_table_config ERROR: Input/output error (-5)
attr 6: dcxo_tune_fine ERROR: No such device (-19)
attr 7: dcxo_tune_fine_available value: [0 0 0]
attr 8: ensm_mode_available value: sleep wait alert fdd pinctrl pinctrl_fdd_indep
attr 9: multichip_sync ERROR: Permission denied (-13)
attr 10: rssi_gain_step_error value: lna_error: 0 0 0 0
mixer_error: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
gain_step_calib_reg_val: 0 0 0 0 0
attr 11: dcxo_tune_coarse_available value: [0 0 0]
attr 12: tx_path_rates value: BBPLL:983039994 DAC:122879999 T2:122879999 T1:61439999 TF:30719999 TXSAMP:30719999
attr 13: trx_rate_governor_available value: nominal highest_osr
attr 14: xo_correction value: 40000140
attr 15: ensm_mode value: fdd
attr 16: filter_fir_config value: FIR Rx: 0,0 Tx: 0,0
attr 17: calib_mode value: auto
175 debug attributes found:
debug attr 0: digital_tune value: 0
debug attr 1: calibration_switch_control value: 0
debug attr 2: multichip_sync value: 0
debug attr 3: gaininfo_rx2 ERROR: Resource temporarily unavailable (-11)
debug attr 4: gaininfo_rx1 value: 71 76 0 0 0 0 0 0
debug attr 5: bist_timing_analysis value: 0
debug attr 6: bist_tone value: 0
debug attr 7: bist_prbs value: 0
debug attr 8: loopback value: 0
debug attr 9: initialize value: 0
debug attr 10: adi,txmon-2-lo-cm value: 48
debug attr 11: adi,txmon-1-lo-cm value: 48
debug attr 12: adi,txmon-2-front-end-gain value: 2
debug attr 13: adi,txmon-1-front-end-gain value: 2
debug attr 14: adi,txmon-duration value: 8192
debug attr 15: adi,txmon-delay value: 511
debug attr 16: adi,txmon-one-shot-mode-enable value: 0
debug attr 17: adi,txmon-dc-tracking-enable value: 0
debug attr 18: adi,txmon-high-gain value: 24
debug attr 19: adi,txmon-low-gain value: 0
debug attr 20: adi,txmon-low-high-thresh value: 37000
debug attr 21: adi,gpo3-tx-delay-us value: 0
debug attr 22: adi,gpo3-rx-delay-us value: 0
debug attr 23: adi,gpo2-tx-delay-us value: 0
debug attr 24: adi,gpo2-rx-delay-us value: 0
debug attr 25: adi,gpo1-tx-delay-us value: 0
debug attr 26: adi,gpo1-rx-delay-us value: 0
debug attr 27: adi,gpo0-tx-delay-us value: 0
debug attr 28: adi,gpo0-rx-delay-us value: 0
debug attr 29: adi,gpo3-slave-tx-enable value: 0
debug attr 30: adi,gpo3-slave-rx-enable value: 0
debug attr 31: adi,gpo2-slave-tx-enable value: 0
debug attr 32: adi,gpo2-slave-rx-enable value: 0
debug attr 33: adi,gpo1-slave-tx-enable value: 0
debug attr 34: adi,gpo1-slave-rx-enable value: 0
debug attr 35: adi,gpo0-slave-tx-enable value: 0
debug attr 36: adi,gpo0-slave-rx-enable value: 0
debug attr 37: adi,gpo3-inactive-state-high-enable value: 0
debug attr 38: adi,gpo2-inactive-state-high-enable value: 0
debug attr 39: adi,gpo1-inactive-state-high-enable value: 0
debug attr 40: adi,gpo0-inactive-state-high-enable value: 0
debug attr 41: adi,gpo-manual-mode-enable-mask value: 0
debug attr 42: adi,gpo-manual-mode-enable value: 0
debug attr 43: adi,aux-dac2-tx-delay-us value: 0
debug attr 44: adi,aux-dac2-rx-delay-us value: 0
debug attr 45: adi,aux-dac2-active-in-alert-enable value: 0
debug attr 46: adi,aux-dac2-active-in-tx-enable value: 0
debug attr 47: adi,aux-dac2-active-in-rx-enable value: 0
debug attr 48: adi,aux-dac2-default-value-mV value: 0
debug attr 49: adi,aux-dac1-tx-delay-us value: 0
debug attr 50: adi,aux-dac1-rx-delay-us value: 0
debug attr 51: adi,aux-dac1-active-in-alert-enable value: 0
debug attr 52: adi,aux-dac1-active-in-tx-enable value: 0
debug attr 53: adi,aux-dac1-active-in-rx-enable value: 0
debug attr 54: adi,aux-dac1-default-value-mV value: 0
debug attr 55: adi,aux-dac-manual-mode-enable value: 1
debug attr 56: adi,aux-adc-decimation value: 256
debug attr 57: adi,aux-adc-rate value: 40000000
debug attr 58: adi,temp-sense-decimation value: 256
debug attr 59: adi,temp-sense-periodic-measurement-enable value: 1
debug attr 60: adi,temp-sense-offset-signed value: 206
debug attr 61: adi,temp-sense-measurement-interval-ms value: 1000
debug attr 62: adi,elna-gaintable-all-index-enable value: 0
debug attr 63: adi,elna-rx2-gpo1-control-enable value: 0
debug attr 64: adi,elna-rx1-gpo0-control-enable value: 0
debug attr 65: adi,elna-bypass-loss-mdB value: 0
debug attr 66: adi,elna-gain-mdB value: 0
debug attr 67: adi,elna-settling-delay-ns value: 0
debug attr 68: adi,ctrl-outs-enable-mask value: 255
debug attr 69: adi,ctrl-outs-index value: 0
debug attr 70: adi,rssi-duration value: 1000
debug attr 71: adi,rssi-wait value: 1
debug attr 72: adi,rssi-delay value: 1
debug attr 73: adi,rssi-unit-is-rx-samples-enable value: 0
debug attr 74: adi,rssi-restart-mode value: 3
debug attr 75: adi,fagc-adc-large-overload-inc-steps value: 2
debug attr 76: adi,fagc-power-measurement-duration-in-state5 value: 64
debug attr 77: adi,fagc-rst-gla-if-en-agc-pulled-high-mode value: 0
debug attr 78: adi,fagc-rst-gla-en-agc-pulled-high-enable value: 0
debug attr 79: adi,fagc-rst-gla-large-lmt-overload-enable value: 1
debug attr 80: adi,fagc-rst-gla-large-adc-overload-enable value: 1
debug attr 81: adi,fagc-energy-lost-stronger-sig-gain-lock-exit-cnt value: 8
debug attr 82: adi,fagc-rst-gla-engergy-lost-sig-thresh-below-ll value: 10
debug attr 83: adi,fagc-rst-gla-engergy-lost-goto-optim-gain-enable value: 1
debug attr 84: adi,fagc-rst-gla-engergy-lost-sig-thresh-exceeded-enable value: 1
debug attr 85: adi,fagc-rst-gla-stronger-sig-thresh-above-ll value: 10
debug attr 86: adi,fagc-optimized-gain-offset value: 5
debug attr 87: adi,fagc-rst-gla-stronger-sig-thresh-exceeded-enable value: 1
debug attr 88: adi,fagc-use-last-lock-level-for-set-gain-enable value: 1
debug attr 89: adi,fagc-gain-index-type-after-exit-rx-mode value: 0
debug attr 90: adi,fagc-gain-increase-after-gain-lock-enable value: 0
debug attr 91: adi,fagc-final-overrange-count value: 3
debug attr 92: adi,fagc-lmt-final-settling-steps value: 1
debug attr 93: adi,fagc-lpf-final-settling-steps value: 1
debug attr 94: adi,fagc-lock-level-gain-increase-upper-limit value: 5
debug attr 95: adi,fagc-lock-level-lmt-gain-increase-enable value: 1
debug attr 96: adi,fagc-lp-thresh-increment-steps value: 1
debug attr 97: adi,fagc-lp-thresh-increment-time value: 5
debug attr 98: adi,fagc-allow-agc-gain-increase-enable value: 0
debug attr 99: adi,fagc-state-wait-time-ns value: 260
debug attr 100: adi,fagc-dec-pow-measurement-duration value: 64
debug attr 101: adi,agc-immed-gain-change-if-large-lmt-overload-enable value: 0
debug attr 102: adi,agc-immed-gain-change-if-large-adc-overload-enable value: 0
debug attr 103: adi,agc-gain-update-interval-us value: 1000
debug attr 104: adi,agc-sync-for-gain-counter-enable value: 0
debug attr 105: adi,agc-dig-gain-step-size value: 4
debug attr 106: adi,agc-dig-saturation-exceed-counter value: 3
debug attr 107: adi,agc-lmt-overload-large-inc-steps value: 2
debug attr 108: adi,agc-lmt-overload-small-exceed-counter value: 10
debug attr 109: adi,agc-lmt-overload-large-exceed-counter value: 10
debug attr 110: adi,agc-adc-lmt-small-overload-prevent-gain-inc-enable value: 0
debug attr 111: adi,agc-adc-large-overload-inc-steps value: 2
debug attr 112: adi,agc-adc-large-overload-exceed-counter value: 10
debug attr 113: adi,agc-adc-small-overload-exceed-counter value: 10
debug attr 114: adi,agc-outer-thresh-low-inc-steps value: 2
debug attr 115: adi,agc-outer-thresh-low value: 18
debug attr 116: adi,agc-inner-thresh-low-inc-steps value: 1
debug attr 117: adi,agc-inner-thresh-low value: 12
debug attr 118: adi,agc-inner-thresh-high-dec-steps value: 1
debug attr 119: adi,agc-inner-thresh-high value: 10
debug attr 120: adi,agc-outer-thresh-high-dec-steps value: 2
debug attr 121: adi,agc-outer-thresh-high value: 5
debug attr 122: adi,agc-attack-delay-extra-margin-us value: 1
debug attr 123: adi,mgc-split-table-ctrl-inp-gain-mode value: 0
debug attr 124: adi,mgc-dec-gain-step value: 2
debug attr 125: adi,mgc-inc-gain-step value: 2
debug attr 126: adi,mgc-rx2-ctrl-inp-enable value: 0
debug attr 127: adi,mgc-rx1-ctrl-inp-enable value: 0
debug attr 128: adi,gc-use-rx-fir-out-for-dec-pwr-meas-enable value: 0
debug attr 129: adi,gc-max-dig-gain value: 15
debug attr 130: adi,gc-dig-gain-enable value: 0
debug attr 131: adi,gc-low-power-thresh value: 24
debug attr 132: adi,gc-dec-pow-measurement-duration value: 8192
debug attr 133: adi,gc-lmt-overload-low-thresh value: 704
debug attr 134: adi,gc-lmt-overload-high-thresh value: 800
debug attr 135: adi,gc-adc-large-overload-thresh value: 58
debug attr 136: adi,gc-adc-small-overload-thresh value: 47
debug attr 137: adi,gc-adc-ovr-sample-size value: 4
debug attr 138: adi,gc-rx2-mode value: 2
debug attr 139: adi,gc-rx1-mode value: 2
debug attr 140: adi,update-tx-gain-in-alert-enable value: 0
debug attr 141: adi,tx-attenuation-mdB value: 10000
debug attr 142: adi,rf-tx-bandwidth-hz value: 18000000
debug attr 143: adi,rf-rx-bandwidth-hz value: 18000000
debug attr 144: adi,qec-tracking-slow-mode-enable value: 0
debug attr 145: adi,dc-offset-count-low-range value: 50
debug attr 146: adi,dc-offset-count-high-range value: 40
debug attr 147: adi,dc-offset-attenuation-low-range value: 5
debug attr 148: adi,dc-offset-attenuation-high-range value: 6
debug attr 149: adi,dc-offset-tracking-update-event-mask value: 5
debug attr 150: adi,clk-output-mode-select value: 0
debug attr 151: adi,trx-synthesizer-target-fref-overwrite-hz value: 80008000
debug attr 152: adi,rx1-rx2-phase-inversion-enable value: 0
debug attr 153: adi,tx-rf-port-input-select-lock-enable value: 1
debug attr 154: adi,rx-rf-port-input-select-lock-enable value: 1
debug attr 155: adi,tx-rf-port-input-select value: 0
debug attr 156: adi,rx-rf-port-input-select value: 0
debug attr 157: adi,split-gain-table-mode-enable value: 0
debug attr 158: adi,1rx-1tx-mode-use-tx-num value: 1
debug attr 159: adi,1rx-1tx-mode-use-rx-num value: 1
debug attr 160: adi,2rx-2tx-mode-enable value: 0
debug attr 161: adi,digital-interface-tune-fir-disable value: 1
debug attr 162: adi,digital-interface-tune-skip-mode value: 0
debug attr 163: adi,tx-fastlock-pincontrol-enable value: 0
debug attr 164: adi,rx-fastlock-pincontrol-enable value: 0
debug attr 165: adi,rx-fastlock-delay-ns value: 0
debug attr 166: adi,tx-fastlock-delay-ns value: 0
debug attr 167: adi,tdd-skip-vco-cal-enable value: 0
debug attr 168: adi,tdd-use-dual-synth-mode-enable value: 0
debug attr 169: adi,debug-mode-enable value: 0
debug attr 170: adi,ensm-enable-txnrx-control-enable value: 0
debug attr 171: adi,ensm-enable-pin-pulse-mode-enable value: 0
debug attr 172: adi,frequency-division-duplex-independent-mode-enable value: 0
debug attr 173: adi,frequency-division-duplex-mode-enable value: 1
debug attr 174: direct_reg_access value: 0x0
iio:device4: cf-ad9361-lpc (buffer capable)
2 channels found:
voltage0: (input, index: 0, format: le:S12/16>>0)
6 channel-specific attributes found:
attr 0: calibphase value: 0.000000
attr 1: calibbias value: 0
attr 2: calibscale value: 1.000000
attr 3: samples_pps ERROR: No such device (-19)
attr 4: sampling_frequency_available value: 30719999 3839999
attr 5: sampling_frequency value: 30719999
voltage1: (input, index: 1, format: le:S12/16>>0)
6 channel-specific attributes found:
attr 0: calibbias value: 0
attr 1: calibphase value: 0.000000
attr 2: calibscale value: 1.000000
attr 3: samples_pps ERROR: No such device (-19)
attr 4: sampling_frequency_available value: 30719999 3839999
attr 5: sampling_frequency value: 30719999
2 debug attributes found:
debug attr 0: pseudorandom_err_check value: CH0 : PN9 : Out of Sync : PN Error
CH1 : PN9 : Out of Sync : PN Error
debug attr 1: direct_reg_access value: 0x0
iio:device2: xadc
10 channels found:
voltage5: vccoddr (input)
2 channel-specific attributes found:
attr 0: scale value: 0.732421875
attr 1: raw value: 1848
voltage0: vccint (input)
2 channel-specific attributes found:
attr 0: raw value: 1385
attr 1: scale value: 0.732421875
voltage4: vccpaux (input)
2 channel-specific attributes found:
attr 0: scale value: 0.732421875
attr 1: raw value: 2455
temp0: (input)
3 channel-specific attributes found:
attr 0: scale value: 123.040771484
attr 1: offset value: -2219
attr 2: raw value: 2646
voltage7: vrefn (input)
2 channel-specific attributes found:
attr 0: scale value: 0.732421875
attr 1: raw value: 8
voltage1: vccaux (input)
2 channel-specific attributes found:
attr 0: scale value: 0.732421875
attr 1: raw value: 2457
voltage2: vccbram (input)
2 channel-specific attributes found:
attr 0: scale value: 0.732421875
attr 1: raw value: 1377
voltage3: vccpint (input)
2 channel-specific attributes found:
attr 0: scale value: 0.732421875
attr 1: raw value: 1377
voltage8: (input)
2 channel-specific attributes found:
attr 0: raw value: 3693
attr 1: scale value: 0.244140625
voltage6: vrefp (input)
2 channel-specific attributes found:
attr 0: raw value: 1711
attr 1: scale value: 0.732421875
1 device-specific attributes found:
attr 0: sampling_frequency value: 961538
iio:device0: adm1177
2 channels found:
voltage0: (input)
2 channel-specific attributes found:
attr 0: scale value: 6.433105468
attr 1: raw value: 769
current0: (input)
2 channel-specific attributes found:
attr 0: raw value: 805
attr 1: scale value: 0.516601562
コマンドラインで