ワンセグ生データをOFDM復調(2)
前回までで、ワンセグの生データからのOFDMシンボル切り出しあたりまで実装しました。今回はそれ以降の処理についてです。
前提知識
ワンセグも含めて、地上波デジタル放送は、ARIBにて規格書が配布されています。
標準規格(放送分野)一覧表のSTD-B31「地上デジタルテレビジョン放送の伝送方式」から入手可能です。私は会員でもないので、英語版を入手しています。
FFT以降の処理
前回の部分も少し修正して[11]については、次のようにしました。
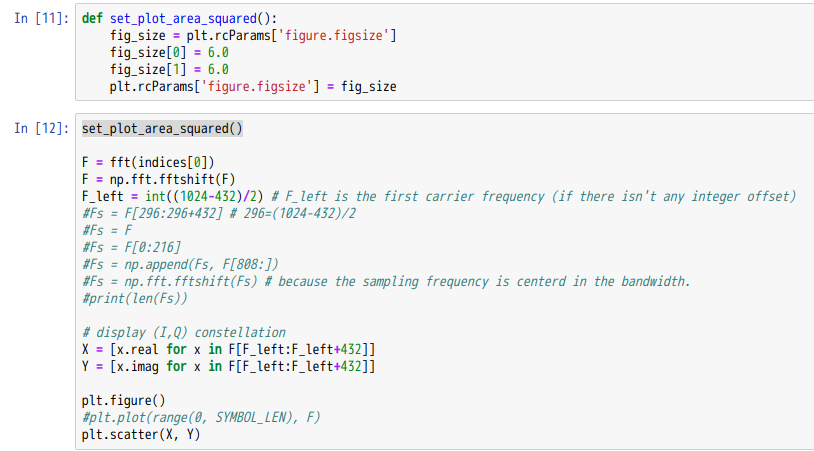
重要なのはfftshiftを実施していることです。データ取得時のサンプリング周波数は、放送帯域の中心に設定しているので、(キャリア周波数オフセットが0であれば)fftshift後の配列中央の値が、放送帯域の中心キャリアになるはずです。
また、後でキャリア周波数の整数倍の補正をするために、周波数シフトをする必要があります。そのためのシフト量を保持するために、F_leftという変数を定義しています。シフト量が0であった場合に、FFT結果Fのうちキャリア番号0に対応する値を、初期値として設定しています。
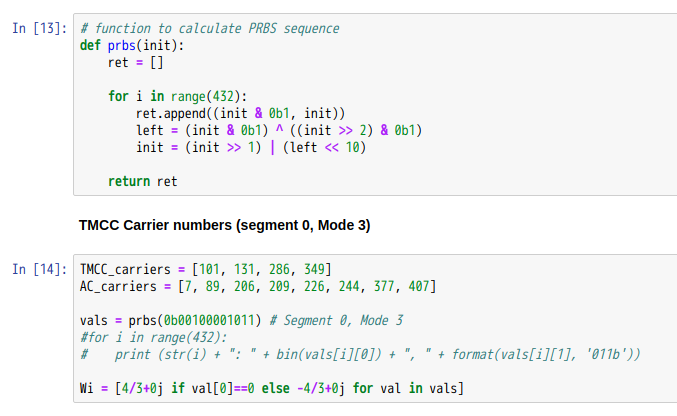
パイロット信号を検出するためにPRBSが必要になるので、その定義と、TMCC、ACという特別なパイロット信号のキャリア番号を定義しています。PRBSの最初の値がキャリア0に、次の値がキャリア1に、…というように、432本のキャリアにそれぞれ0, 1のいずれかが対応します。SP(Scattered Pilot)信号は、このキャリア周波数毎の0, 1の値がBPSKにより、IQ空間上のそれぞれ(+4/3, 0), (-4/3, 0)にマップされます。これを上記では配列Wiで定義しています。
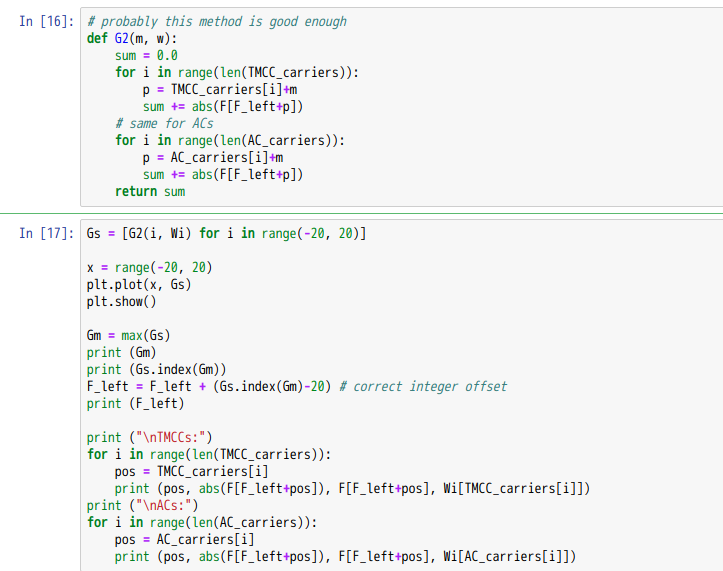
上記は、TMCCとACの場所を推定するための関数です。G2では、引数mで指定された分だけ、キャリア周波数を移動した場所をTMCC, ACとみなして、絶対値の積算をしています。
Gs = [G2(i, Wi) for i in range(-20, 20)]
にて、キャリア周波数を-20から20まで整数倍シフトして、G2の積算値が最大になる場所を求めます。最大値が得られるインデックスでF_leftを調整しています。これでキャリア番号0から431までの場所が求まったことになるはずです。上記のプロット結果は省略します。
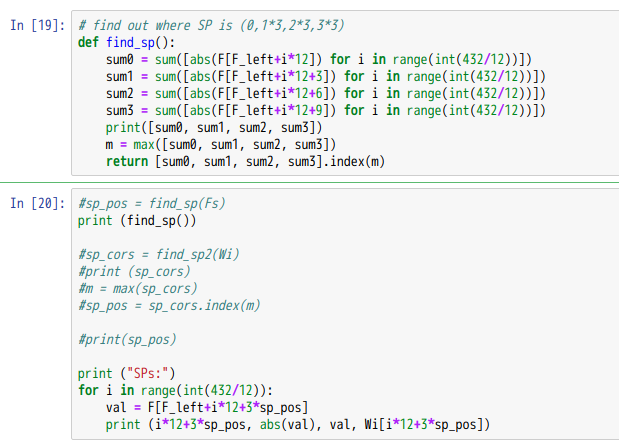
次はSPの推定です。SP信号は12キャリアに1本あります。OFDMシンボル毎に場所が3キャリアずつ移動します。つまり、OFDMシンボル毎に、SPの場所はi12, i12+3, i12+6, i12+9, i*12,…のように巡回します。上記find_spでは、現OFDMシンボルでSPが何処に含まれているかを求めています。SPは、それ以外のデータキャリアに比べて4/3倍の絶対値を持っているので、上記のように積算した最大値を求めるという方法が使えます。
ここからがまだうまく行っていないと思われるのですが、上記では次のような出力が得られます(行が長くなりすぎるので、小数点以下は一部省略しています)。
[35.74547, 36.26827, 49.57394, 37.08745]
2
SPs:
6 1.0953 (-0.9832743533464458+0.482584084887267j) 1.3333
18 1.1773 (0.9411424714348882-0.7073685094875273j) 1.3333
30 1.2927 (0.9226357042956151-0.905485176200131j) -1.3333
42 1.3544 (-0.9451630023246448+0.9701050133998432j) -1.3333
54 1.3868 (-1.041607866189769+0.9155528236391836j) 1.3333
66 1.2944 (0.6906246945088386-1.0947704458085812j) 1.3333
78 1.0671 (0.6685409527954194-0.8316726977365281j) -1.3333
90 1.3859 (0.7967161344290873-1.1339926757265295j) 1.3333
102 1.1538 (-0.34105207413393135+1.102293053251151j) 1.3333
114 1.2401 (0.4762959068094629-1.144985106068488j) 1.3333
126 1.5607 (0.725557306133454-1.381834432391039j) -1.3333
138 1.2347 (-0.6547734652174335+1.0467712733713745j) -1.3333
150 1.3194 (-0.3329626554307+1.2767023965626096j) 1.3333
162 1.5988 (0.5091991640004263-1.5155690510396185j) 1.3333
174 1.3907 (-0.6562514301534865+1.2261640531390314j) 1.3333
186 1.6392 (-0.5092859972519473+1.5580715920605588j) -1.3333
198 1.5107 (0.26879055172568034-1.4866408415508643j) -1.3333
210 1.6382 (0.7524038499463859-1.4552230916819244j) 1.3333
222 1.3896 (0.44737449638796445-1.3156195604230028j) -1.3333
234 1.3833 (0.5356609612670982-1.2753992069341795j) 1.3333
246 1.559 (0.3497743406085074-1.5192501362727482j) -1.3333
258 1.1333 (-0.42997707286624176+1.048549775299747j) -1.3333
270 1.3702 (-0.2787479092644133+1.3415065163031206j) 1.3333
282 1.6204 (-0.5708941597565+1.5164865623719384j) -1.3333
294 1.4883 (0.6930350159378798-1.317100025661765j) -1.3333
306 1.5654 (-0.7261325631313592+1.3867477986830758j) -1.3333
318 1.5449 (0.4601928773417365-1.4747525850693373j) -1.3333
330 1.4912 (0.5746828035844906-1.3760673756943445j) 1.3333
342 1.4701 (0.825690594740095-1.2162618274644958j) -1.3333
354 1.4209 (0.24893414863314506-1.398884931842842j) 1.3333
366 1.3512 (-0.6292706725628592+1.1957269229318115j) 1.3333
378 1.4125 (-0.5413499265712505+1.3046784927444803j) -1.3333
390 1.4662 (0.7501030028129436-1.2598034492601253j) -1.3333
402 1.1753 (-0.7940964094918974+0.8664208985515854j) -1.3333
414 1.3589 (-0.7997872953740967+1.098570575241878j) 1.3333
426 1.0329 (-0.3727620060886928+0.96334271774669j) -1.3333
最初の行と次の行は、SPの場所と絶対値の積算値を表示しています。49は残りの3つの値36付近に比べると、ほぼ4/3倍となっているので、結果は正しそうに思われます。
ただ、それ以降、SPのキャリア番号と絶対値、その値、また、期待される値を各行表示していますが、 これがおかしいと思われます。例えば、キャリア番号6は、値が第2象限である一方、期待される値は(4/3, 0)です。次に、キャリア番号18では、値が第4象限である一方、こちらも期待される値は(4/3, 0)です。つまり、この結果が正しいのであれば、キャリア番号6と18とで、チャンネルの影響で回転した方向が逆になってしまっています。
しかも、よく観察すると、この結果は、キャリア番号6+24nと18+24nとでいつも成り立っているようです。つまり、回転方向がこれら2つの間でいつも逆です。
さらに、上記SPを実際にプロットした結果が次です。
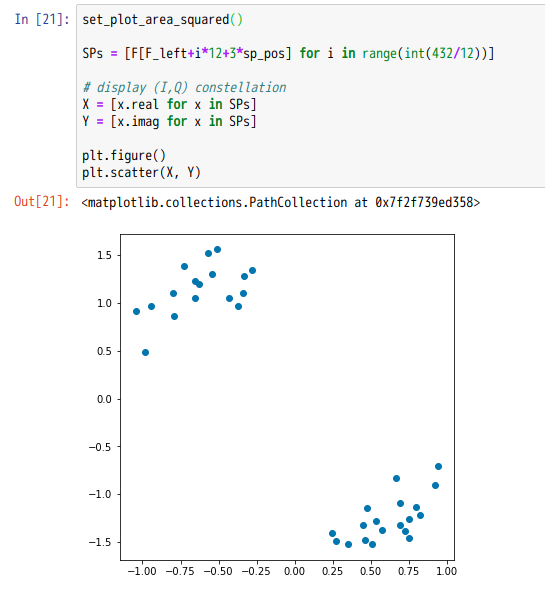
この表示自体は、実数軸上にあるSPがどちらかに回転したと考えれば、それなりの結果に見えます。 ただ、上記の通り、回転方向がいつも逆になっているので、恐らくどこかに間違いがあるはずです。 現在のところここで躓いています。これだと、単純に残りのキャリアの推定を線形補間で行うと、絶対値が0近辺の値が出てきてしまうことになり、正しく補正できません。チャンネル推定をして補正を行う前に、上記の問題を解決する必要があります。