前回までで、ワンセグの生データからのOFDMシンボル切り出し、パイロット信号を見つけるところまで実装しました。ところが、パイロット信号からチャンネル補正ができそうにない、というところで止まってしまいました。もう少し調査したところ、原因が分かってきました。 自分の理解の範囲でのまとめです。

OFDM Baseband Receiver Design for Wireless CommunicationsのChanter 5. Synchronizationの式(5.6)は次のようになっています。

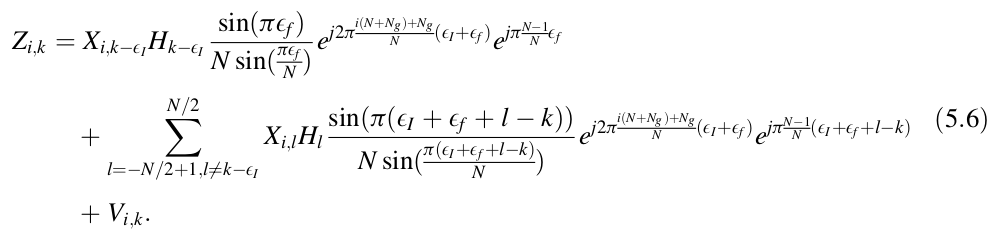
これは、キャリア周波数のオフセットが、FFTした結果に及ぼす影響を記述した式です。 左辺Z_{i, k}は、(時系列に並んだ)i番目のシンボルの、k番目のサブキャリアの(周波数領域の)値を示しています。また、ε_I, ε_fがそれぞれキャリア周波数オフセットの整数部、小数部です。 Hはそれぞれのサブキャリアに対応するチャンネルの周波数応答です。

ごちゃごちゃしていますが、とにかく、ε_I, ε_fが0でなければ、Z = X Hとは記述できず、他のキャリア周波数の影響を受けてしまうことを示しています。

右辺の第一項を見てみると、大きく4つの掛け算になっていますが、最後の2つのe^{…}の部分は純粋な回転です。 これまでの実装で、小数部のキャリア周波数補正はできていると思われます。 そのため、ε_fはほとんど0と考えます。

したがって、振幅だけを見るならば、受信したk番目のサブキャリアのFFT結果は、送信側のk-ε_I番目のサブキャリアの値に、チャンネル応答を掛けたものになっています(sinの項はε_f->0で1になるため)。 ですから、パイロット信号も含めてXの振幅は既知なので、振幅について積算することで、 ε_Iを求めることができたのでした。

問題は3番目のeの項による回転です。 この式を見るとε_Iが0でなければ、時間と共に盛大に回転します。 (2019/2/20追記：これ自体は正しいですが、kには依存していませんので、 Scattered Pilotがキャリアによって回転量が異なることの説明にはなりません。 それより(5.6)右辺第2項が寄与しているのかも知れません)

これの逆数を求めて回転を補正することもできるかも知れませんが、 上記の式では右辺には第2項以降も存在します。 そのため、基本的にはε_I, ε_fを0に収束させるような制御をしたほうが良さそうです。

上記の本の5.2.3節にも、周波数領域の推定アルゴリズムには限度があるので、同期エラーはその限界内に来ていることを確かめないといけない、といった記述があります。そのためには、時間領域で補正することができる、と書かれています。

時間領域での補正方法は下記の図のようになります(Figure 5.13より)。

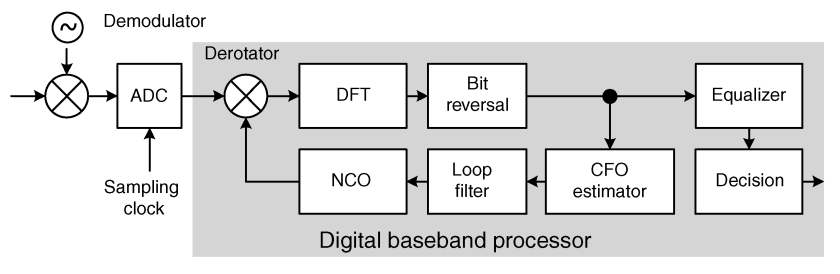
求められたε_I, ε_fをloop filterを通してNCOに与え、その周波数でサンプリングしたデータを回転させる、というものです。 これまでの実装ではε_fのみしか考慮していませんでしたが、ε_Iも考慮する必要がある、ということです。

以上を参考にして、PLLでキャリア周波数オフセットを0に制御できるか試してみたいと思います。